Opis
P1.5.1 Wahadło proste i złożone – Leybold
P1.5.1.1 Wyznaczanie przyspieszenia ziemskiego przy pomocy prostego wahadła
P1.5.1.3 Drgania pręta wahadła
P1.5.1.2 Wyznaczanie przyspieszenia ziemskiego przy pomocy wahadła odwracalnego
P1.5.1.4 Zależność okresu drgań pręta wahadła od amplitudy
P1.5.1.5 Określenie przyspieszenia grawitacji na ziemi za pomocą pręta wahadła
P1.5.1.6 Wahadło ze zmiennym przyspieszeniem ziemskim (wahadło zmienne-g)
Poprzez wahadło proste lub “matematyczne” rozumiemy masę punktową m zawieszoną na nici o masie zerowej i długości s.
Tym samym, wahadło matematyczne może teoretycznie zostać użyte go precyzyjnego wyznaczenia przyspieszenia grawitacyjnego g poprzez pomiar okresu oscylacji i długości wahadła.
W doświadczeniu P1.5.1.1, kula z zawieszeniem wahadłowym jest użyta do wyznaczenia przyspieszenia grawitacyjnego. Jako, że masa kuli jest dużo większa niż stalowego drutu, na którym jest zawieszona, wahadło to może być uznane za bliskie przybliżenie wahadła matematycznego. Rejestrowane są wielokrotne oscylacje, aby zwiększyć dokładność pomiaru. Dla przyspieszenia grawitacyjnego, błąd zależy od podstawowej dokładności, z jaką wyznaczana jest długość wahadła.
Wahadło rewersyjne użyte w doświadczeniu P1.5.1.2 ma dwie krawędzie do zawieszenia wahadła i dwóch odważników ślizgowych do “strojenia” okresu oscylacji.
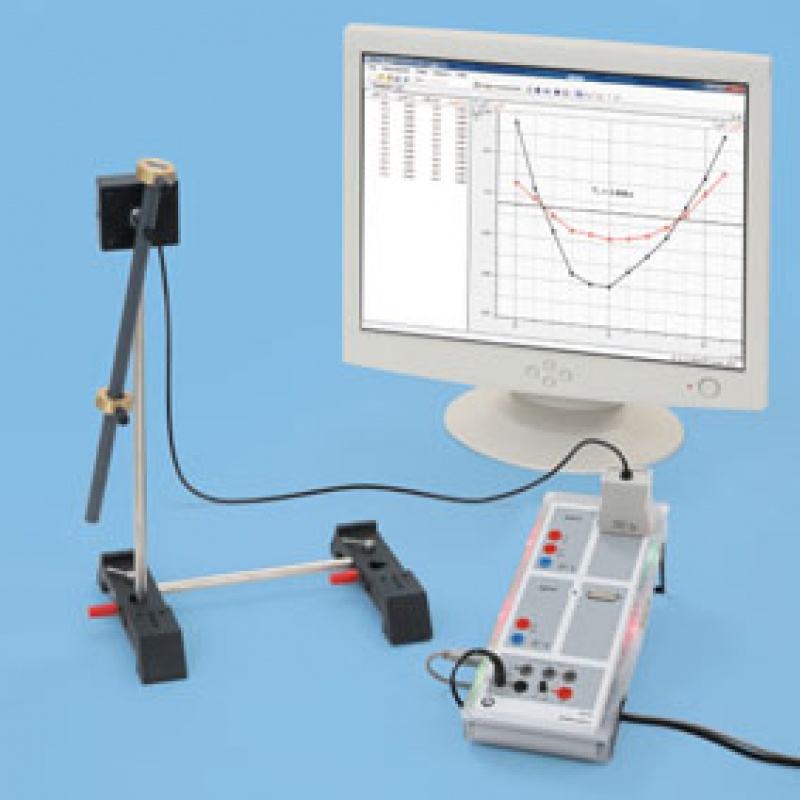
W doświadczeniu P1.5.1.3, oscylacje wahadła prętowego, tj. badane jest proste wahadło fizyczne. Korzystając z czujnika ruchu obrotowego S oscylacje wahadła są rejestowane jako funkcja czasu. Porównywane jest kąt a(t), prędkość w(t) oraz przyspieszenie a(t). Dodatkowo, długość obliczeniowa wahadła jest wyznaczana ze zmierzonego okresu oscylacji T.
W doświadczeniu P1.5.1.4, badana jest zależność okresu T na amplitudę A oscylacji. Dla małych odchyleń oscylacje wahadła są w przybliżeniu harmoniczne i okres jest niezależny od amplitudy. Dla dużych wychyleń to przybliżenie nie jest spełnione: im większa amplituda tym większy okres.
W doświadczeniu P1.5.1.5, wahadło prętowe jest zastosowane jako wahadło rewersyjne. Wyznaczana jest wartość przyspieszenia spowodowanego grawitacją.
Wahadło jest ustawione w dwóch punktach podparcia po przeciwnych stronach pręta. Położenie dwóch ciężarków ślizgowych wpływa na okres. Gdy wahadło jest poprawnie nastawione, oscyluje na obu krawędziach z tym samym okresem T. Długość obliczeniowa wahadła lr odpowiada odległości d pomiędzy dwoma punktami podporu. Przyspieszenie spowodowane grawitacją jest obliczane z długości obliczeniowej wahadła lr i okresu T.
W doświadczeniu P1.5.1.6, zmontowane i badane jest wahadło ze zmiennym przyspieszeniem spowodowanym grawitacją (zmienne wahadło g). Płaszczyzna oscylacji jest pochylona. Tym samym, przyspieszenie grawitacyjne jest zredukowane. Prowadzi to do różnych okresów oscylacji zależnie od pochylenia. W doświadczeniu wyznaczana jest zależność okresu na kąt pochylenia. Dodatkowo, symulowane jest przyspieszenie spowodowane grawitacją na różnych ciałach niebieskich.